Question

Water flows in a canal of trapezoidal cross section with a depth of 5 feet and side slopes are at 40 degrees and a bottom width of 12 feet.

The bottom drops 1.4 ft per 1000 ft of length.

The canal is lined with smooth concrete with a friction coefficient of 0.012.

Determine the Froude number of this channel.

Answer 1

We will proceed to find the Froude number through the geometric figure raised in the attached graphic. This graph will allow us to more easily extract the data concerning the distance x, the width of the upper part and the area of the object.

With the geometric data you can find the hydraulic radius and the hydraulic depth: Variables to find the Froude number.

`tan40 = (x)/(5)`

`x = 4.195ft`

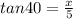
The top Width is given as,

`width = 2(4.195)+12 = 20.39'`

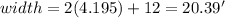
Now the Area:

`A= (1)/(2) 5 (12+20.39) = 80.97ft^2`

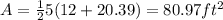
At the same time the Slope Length

`S_l = √(4.195^2+5^2)`

`S_l = 6.52ft`

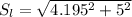
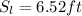
The welted perimeter is given as twice the slope length and the bottom width:

`\phi = (2*6.52)+12`

`\phi = 25.05'`

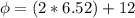
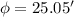
The hydraulic radius is the change of the Area respect the perimeter:

`R = (A)/(\phi)`

`R= (80.97)/(25.05)`

`R= 3.23'`

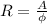
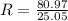
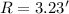
Previously was given the friction coefficient (n) = 0.012 and at the same time the bed slope is equal to the proportion between the bottom drops and its length:

`S_o = (1.4)/(1000)`

From these values the velocity would be:

`V = (1)/(n) R^(2/3)So^(1/2) \Rightarrow (1)/(0.012)*3.23^(2/3)((1.4)/(1000))^(1/2)`

`V= 6.815ft/s`

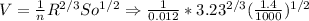
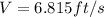
The Hydraulic Depth (D) is equal to

`D = (A)/(Width) = (80.97)/(20.39)`

`D = 3.97'`

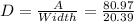
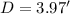
We can now find the Froude's number in function of the velocity, the gravity and the hydraulic Depth:

`Fr = (V)/(gD^(1/2))`

`Fr = (6.815)/((32.17*3.97)^(1/2))`

`Fr = 0.602`

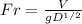
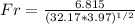
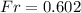
Finally we have that the Freoude number is equal to 0.602