Question

Which description is paired with its correct expression?

four less than the quotient of a number cubed and seven, increased by three; 4-7 +3

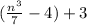
five times the difference of a number squared and six; 516-17']

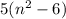
nine more than the quotient of six and a number cubed, decreased by fo

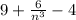
twice the difference of nine and a number squared: 219-

Answer 1

D-twice the difference of nine and a number squared; 2 (9 minus n squared)

Explanation:

Got it right on test

Answer 2

four less than the quotient of a number cubed and seven, increased by three
`((n^3)/(7) -4)+3`

five times the difference of a number squared and six

`5(n^2 -6)`

nine more than the quotient of six and a number cubed, decreased by four

`9+(6)/(n^3)-4`

twice the difference of nine and a number squared

`2(9-n^2)`

Explanation:

Let n the number of interest we have this:

four less than the quotient of a number cubed and seven, increased by three
`((n^3)/(7) -4)+3`

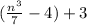
five times the difference of a number squared and six

`5(n^2 -6)`

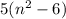
nine more than the quotient of six and a number cubed, decreased by four

`9+(6)/(n^3)-4`

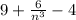
twice the difference of nine and a number squared:

`2(9-n^2)`