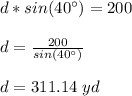Question

2. A ski resort is building a new ski lift that will transport tourists from the base of the mountain to its highest point. This mountain has a vertical height of 200 yards, and the ski lift will rise at an angle of 40 degrees. When the project is completed, how many yards, d, will a tourist travel from the base of the mountain to its peak?

Part I: Sketch a figure to illustrate the scenario above. Label the vertices and the lengths that are given in the question. (3 points)





Part II: Using your sketch from Part I, equation using a trigonometric ratio to find the distance a tourist will travel from the base of the mountain to its peak. Round your answer to the nearest 100th. Show your work. (2 points)

Answer 1

Part I: See the image attached.

Part II:
`d=311.14\ yd`

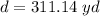
Explanation:

Part I

With the data given in the exercise, you can draw the right triangle shown attached, where the side BC is the height of the mountain (
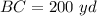`BC=200\ yd`), and the side AB is the distance that the tourist will travel from the base of the mountain to its peak (
`AB=d`).

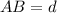Part II

In order to find "d", you need to use the following Trigonometric ratio:

`sin\alpha =(opposite)/(hypotenuse)`

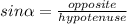
In this case, you can identify from the figure that:

`\alpha=40\°\\\\opposite=BC=200\\\\hypotenuse=AB=d`

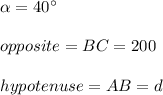
Substitute into
`sin\alpha =(opposite)/(hypotenuse)`:

`sin(40\°)=(200)/(d)`

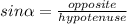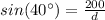
Finally, you must solve for "d" in order to find its value. This is (Rounded to the nearest 100th):

`d*sin(40\°)=200\\\\d=(200)/(sin(40\°))\\\\d=311.14\ yd`