Question

A slender rod 100.00cm long is used as a meter stick. Twoparallel axes which are perpendicular to the rod are considered.The first axis passes through the 50cm mark and the second axispasses through the 30cm mark. The ratio of the moment ofinertia through the second axis to that of the first axis isclosest to:

a. 1.7
b. 2.3
c. 2.1
d. 1.5
e. 1.9

Answer 1

I /
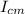`I_(cm)` = 1.48 , The correct answer is d

Step-by-step explanation:

the moment of inertia is given by

I = ∫ r² dm

For figures with symmetry it is tabulated. In the case of a thin variation, the moment of inertia with respect to its center of mass is

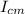`I_(cm)` = 1/12 M L2

There is a widely used theorem, which is the parallel axis theorem, where the moment of inertia of any parallel axis, is the moment of mass inertia plus the moment of inertia of the body taken as a particle

I =
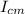`I_(cm)` + M D²

Let's put these expressions to our case.

As the bar is one meter long its center of mass that this Enel midpoint corresponds to

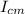`I_(cm)` = 1/12 m L²

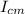`I_(cm)` = 1/12 m 1.00²

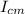`I_(cm)` = 8.33 10⁻² m

Let's use the parallel axes theorem for the axis that passes through x = 30 cm. The distance from the enrode masses to the axis is

D =
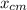`x_(cm)` - 0.30

D = 0.50 - 0.30 = 0.20 m

I =
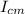`I_(cm)` + m D²

I = 8.33 10⁻² m + m 0.2²

I = (8.33 10⁻² + ​​4 10⁻²) m

I = 12.33 10⁻² m

The relationship between these two moments of inertia

I /
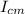`I_(cm)` = 12.333 10⁻² / 8.333 10⁻²

I /
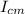`I_(cm)` = 1.48

The correct answer is d