Question

Which equation correctly uses the value of b to solve for a?

tan(22.6o) = StartFraction a Over 13 EndFraction

tan(22.6o) = StartFraction 13 Over a EndFraction

tan(22.6o) = StartFraction a Over 12 EndFraction

tan(22.6o) = StartFraction 12 Over a EndFraction

Answer 1

The answer is C on Edge 2020

Explanation:

Answer 2

`\tan(22.6)=(a)/(12)`

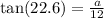
Explanation:

We know that
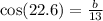`\cos(22.6)=(b)/(13)`. Rounding the value of b as asked in the problem gives b=12.

From the right-triangle definition of cosine, b must be the adjacent side to the angle 22.6º and the hypothenuse of the triangle must be 3.

Then, a is the opposite side of the angle 22.6º therefore using the definition of sine,
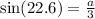`\sin(22.6)=(a)/(3)`. Solving for a, we obtain
`a=3 sin(22.6)=3\cos(22.6)\tan(22.6)=b\tan (22.6)=12\tan(22.6)`.

We conclude that
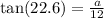`\tan(22.6)=(a)/(12)`.