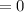Answer:
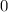
Explanation:
Given the following expression:
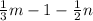
You know that the value of "m" is:
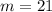
And the value of "n" is:

Knowing these values, you must substitute them into the given expression:
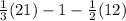
So, in order to evaluate, the first step is to solve the multiplications and then you must reduce the fractions. Then:
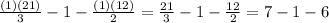
Now, you must solve the subtraction.
You get that the difference (which is the result of the subtraction) is the following: