Question

To test the effect of classical music on the brain, a study has been done. Twenty 6th grade students are randomly divided into two groups of 10 students and the same math test was given to these students. The first group of students listened to classical music for 20 minutes right before taking the test and the other group of students took the test without listening to it. Here are their scores. Assume equal variance for answering the following questions. Group with music: 91 77 58 89 83 78 74 81 91 88 Group without music: 81 65 69 69 67 61 67 87 64 81 Construct a 95% confidence interval of the mean difference. Test if the students who listened to classical music before the test scored higher than the other group of students using alpha = 0.05. Conduct the same test as in part (b) using alpha = 0.01.

Answer 1

Explanation:

Hello!

A study was conducted to test the effect of classical music on the brain. For this 20 6th grade students were randomly divided into two independent groups of 10, the same math test was given to these students. The first group listened to classical music for 20 min before taking the test. The second group took the test without listening to music.

Sample 1 (With music)

X₁: Score of a 6th grade student that heard 20 min classical music before taking the math test.

91 77 58 89 83 78 74 81 91 88

n₁= 10

X[bar]₁= 81

S₁= 10.11

Sample 2 (Without music)

X₂: Score of a 6th grade student that didn't hear classical music before taking the math test.

81 65 69 69 67 61 67 87 64 81

n₂= 10

X[bar]₂= 71.10

S₂= 8.70

Asuming both variables have a normal distribution and the population variances are unknown but equal, the statistic to use for both the CI and hypothesis tests is:

t= (X[bar]₁-X[bar]₂) - (μ₁ - μ₂) ~t
`_(n_1+n_2-2)`

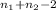
Sa
`\sqrt{(1)/(n_1) + (1)/(n_2) }`

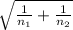
a) 95% for (μ₁ - μ₂)

(X[bar]₁-X[bar]₂) ±
`t_(n_1+n_2-2; 1-\alpha /2)`*Sa
`\sqrt{(1)/(n_1) + (1)/(n_2) }`

`Sa^2= ((n_1-1)S_1^2+(n_2-1)S_2^2))/(n_1+n_2-2)`

`Sa^2= (9*102.22+9*75.66)/(18)`

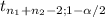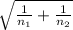
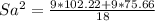
Sa²= 88.94

Sa= 9.4308 ≅ 9.43

`t_(n_1+n_2-2;1-\alpha /2) = t_(18; 0.975) = 2.101`

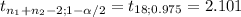
(81-71.10) ± 2.101*(9.43*
`\sqrt{(1)/(10) + (1)/(10) }`)

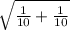[1.04;18.76]

With a confidence level of 95% youd expect that the interval [1.04;18.76] will contain the difference between the population means of the test scores of the kids that listened to classic music and the kids that didn't listen to music before taking the math test.

b)

H₀: μ₁ ≤ μ₂

H₁: μ₁ > μ₂

α: 0.05

One-tailed test (right tail)

Critical value

`t_(n_1+n_2-2; 1 - \alpha ) = t_(18; 0.95) = 1.734`

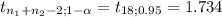
Rejection region t ≥ 1.734

t= (81-71.10) - 0 = 2.34

9.43*
`\sqrt{(1)/(10) + (1)/(10) }`

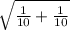
The decision is to reject the null hypothesis.

c) You are asked to conduct the same test at a different levelm this means that only the significance level changes:

H₀: μ₁ ≤ μ₂

H₁: μ₁ > μ₂

α: 0.01

One-tailed test (right tail)

Critical value

`t_(n_1+n_2-2; 1 - \alpha ) = t_(18; 0.99) = 2.552`

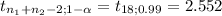
Rejection region t ≥ 2.552

t= (81-71.10) - 0 = 2.34

9.43*
`\sqrt{(1)/(10) + (1)/(10) }`

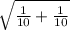
The decision is to not reject the null hypothesis.

At a significance level of 5%, the decision is to reject the null hypothesis, which means that the population average of the test scores of 6th-grade children that listened to classical music before taking a math test is greater than the population average of the test scores of 6th graders that took the math test without listening to classical music.

But at 1% significance level, there is not enough evidence to reject the null hypothesis. At this level, the conclusion is that the average test score of 6th graders that listened to classical music before taking the math test is at most equal to the average test score of 6th graders that didn't listen to music before the test.

I hope it helps!