Answer:
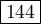
Explanation:
1. Set up the integral.
The equation for the circle is
x² + y² = 9
The bottom corners of the square are at
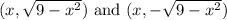
The length (a) of a side is
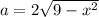
and the area (A) of the square cross-section is
A = a² = 4(9 - x²)
The volume (V) of the solid is
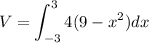
2. Solve the integral
![\displaystyle \int_(-3)^(3) {4(9 - x^(2))} dx = 4\begin{bmatrix}9x - (1)/(3)x^(3)\end{bmatrix}_(-3)^(3)= 4[(27 - 9) - (-27 +9)] = 4[18 - (-18)]\\= 4[18 + 18] = 4 *36 = \mathbf{144}\\\\\text{The volume of the solid is $\large \boxed{\mathbf{144}}$}](https://img.qammunity.org/2020/formulas/mathematics/high-school/doveuye01qregq1bz7ulluotj73bpfj39o.png)