Question

With "normal" gravity, we used a potential energy of mgh. Now with the gravity that is more accurate over longer distances we use a different potential energy. In you own words compare and contrast the two situations. What are the important differences?

Answer 1

A general solution is
`\Delta U=mh(GM)/(r^(2))(r)/(r+\Delta h)` and a particualr case is mgh, it is just to distance around the radius Earth.

Step-by-step explanation:

We can use a general equation of the potential energy to understand the particular and general case:

The potential energy is defined as
`U=-\int F\cdot dx`, we know that the gravitational force is
`F=GmM/r^(2)`, so we could find the potential energy taking the integral of F.

`U=-GmM/r` (1)

We can find the particular case, just finding the gravitational potential energy difference:

`\Delta U=U_(f)-U_(i)`. Here Uf is the potential evaluated in r+Δh and Ui is the potential evaluated in r.

Using (1) we can calculate ΔU.

`\Delta U=-(GmM)/(r+\Delta h)+(GmM)/(r)`

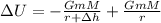
Simplifying and combining terms we have a simplified expression.

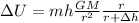`\Delta U=mh(GM)/(r^(2))(r)/(r+\Delta h)` (2)

Let's call
`g=(GM)/(r^(2))`. It is the acceleration due to gravity on the Earth's surface, if r is the radius of Earth and M is the mass of the Earth and we can write (2) as ΔU=mgh, but if we have distance grader than r we should use (2), otherwise, we could get incorrect values of potential energy.

I hope i hleps you!