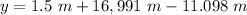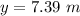Answer:
1)
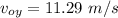
2)
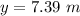
Step-by-step explanation:
Projectile Motion
When an object is launched near the Earth's surface forming an angle
 with the horizontal plane, it describes a well-known path called a parabola. The only force acting (neglecting the effects of the wind) is the gravity, which acts on the vertical axis.
with the horizontal plane, it describes a well-known path called a parabola. The only force acting (neglecting the effects of the wind) is the gravity, which acts on the vertical axis.
The heigh of an object can be computed as

Where
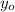 is the initial height above the ground level,
is the initial height above the ground level,
 is the vertical component of the initial velocity and t is the time
is the vertical component of the initial velocity and t is the time
The y-component of the speed is
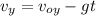
1) We'll find the vertical component of the initial speed since we have not enough data to compute the magnitude of

The object will reach the maximum height when
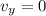 . It allows us to compute the time to reach that point
. It allows us to compute the time to reach that point
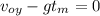
Solving for
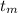
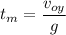
Thus, the maximum heigh is
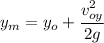
We know this value is 8 meters
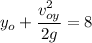
Solving for


Replacing the known values

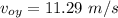
2) We know at t=1.505 sec the ball is above Julie's head, we can compute