Question

The solid rod AB has a diameter dAB 5 60 mm. The pipe CD has an outer diameter of 90 mm and a wall thickness of 6 mm. Knowing that both the rod and the pipe are made of steel for which the allowable shearing stress is 75 MPa, determine the largest torque T that can be applied at A.

Answer 1

3180.86 Nm

Step-by-step explanation:

Moment of inertia for shaft AB,
`I_(AB)= \frac {\pi d^(4)}{32}=\frac {\pi 0.06^(4)}{32}=1.27235* 10^(-6) m^(4)`

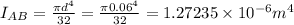
Torque in solid shaft AB will be given by

`T_(AB)=\frac {\tau I_(AB)}{r}=\frac {75* 10^(6) * 1.27235* 10^(-6)}{0.03}=3180.862562 Nm\approx 3180.86 Nm`

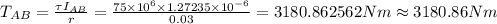
Where
`\tau` is shear stress,
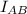`I_(AB)` is polar moment of inertia for shaft AB, r is the radius of shaft B

The inner diameter of pipe CD can found considering that the thickness of pipe is 0.006 m hence diameter= 0.09-(2*0.006)= 0.078 m

Moment of inertia for shaft CD will be

`I_(CD)=\frac {\pi (0.09^(4)-0.078^(4))}{32}=2.8073* 10^(-6) m^(4)`

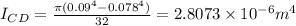
Torque for shaft CD will be

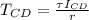`T_(CD) =\frac {\tau I_(CD)}{r}` and here r = 0.045 m

`T_(CD)}=\frac {75* 10^(6) * 2.8073* 10^(-6)}{0.045}=4678.837 Nm\approx 4678.84 Nm`

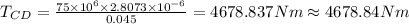
The minimum of the two torques is the largest torque that can be applied. Therefore, the torque to apply equals 3180.86 Nm