Answer:
Perimeter = 27 units
Area = 37.5 sq. units
Explanation:
We have to find the length of all the sides to determine what kind of quadrilateral this is.
Length of AB =

Length of BC =
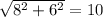
Length of CD =
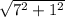 = 5
= 5

Length of DA =
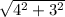 = 5
= 5
The shape is a quadrilateral.
To find the perimeter sum the length of all the sides,
PERIMETER = 5+10+5
 +5 =27 units
+5 =27 units
We can find area by finding areas of triangles separately.
Area of ΔABC = 25 sq. units
Area of ΔACD = 12.5 sq. units
Area of quadrilateral= 25 + 12.5 = 37.5 sq. units