Answer:
Mean: M(x)= 10.2364
Median: Me= 28
Quartiles:
C₁= 14
C₃= 42
Standard deviation S= 3.6715
100% of the respondents have at least 4 pairs of shoes.
Explanation:
Hello!
The study variable is
X: number of pairs of shoes owned by a student
n= 55
xi: 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15
fI: 5; 4; 2; 5; 2; 5; 2; 5; 5; 8; 4 ; 8
You are asked to use this Data to calculate several indexes to summarize it.
The following formulas are for n values ordered in a frequency table, xi= values that the variable take and fi= frequency of the i-value.
Mean M(x):
The arithmetic mean is a central tendency value, that is, it is a position value, it takes values within the variable's definition range but does not necessarily have to correspond to an observed value. It
M(x)= (∑
)*
∑
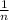
= (4*5)+(5*4)+(6*2)+(7*5)+(8*2)+(9*5)+(10*2)+(11*5)+(12*5)+(13*8)+(14*4)+(15*8)= 563
M(x)= 563*
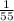= 10.2364
M(x)= 10.2364
Median Me (or 2nd Quartile - C₂-):
The median is also a central tendecy value that divides the sample exactly in a half. This means that 50% of the sample is below the mean and the other 50% is above it.
The formula for odd numbers.
Me=
=
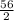
Me= 28
Quartiles:
The quartiles are values of position.
The first Quartile (C₁) indicates the first quarter of the sample. Below this quartile, you find 25% of the values of the variable and above it, you find the other 75%. (25th percentile)
C₁=
=
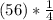= 14
The third Quartile (C₃) indicates the third quarter of the sample, below this number, is the 75% of the sample and above it is the other 25% (75th percentile)
C₃=
=
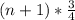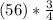= 42
Standard deviation S:
The standard deviation is the square root of the variance. The variance is a measure of dispersion, it indicates the degree of separation of the observed values concerning its arithmetic mean.
S= √S²
S²=
*[∑
-
]
∑
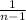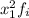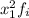= (4²*5)+(5²*4)+(6²*2)+(7²*5)+(8²*2)+(9²*5)+(10²*2)+(11²*5)+(12²*5)+(13²*8)+(14²*4)+(15²*8)= 6491
S²=
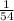*[6491-
]
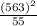S²= 13.4801
S= 3.6715
What percent of the respondents have at least 4 pairs of Shoes?
You could rephrase this as "% of students that have a minimum of 4 pairs of Shoes"
Symbolically: P(X ≥ 4)
To calculate this you have to calculate the punctual probability of each observed value and then the cumulative probabilities for the sample.
The punctual probability for each value of the variable is calculated as P(xi)= xi/n
Cummulative probabilities F(xi) = ∑P(xi)
xi ; fi ; P(xi) ; F(xi) = P(X ≤ xi)
04 ; 5 ; 0.0909 ; 0.0909
05 ; 4 ; 0.0727 ; 0.1636
06 ; 2 ; 0.0364 ; 0.2
07 ; 5 ; 0.0909 ; 0.2909
08 ; 2 ; 0.0364 ; 0.3273
09 ; 5 ; 0.0909 ; 0.4182
10 ; 2 ; 0.0364 ; 0.4546
11 ; 5 ; 0.0909 ; 0.5455
12 ; 5 ; 0.0909 ; 0.6364
13 ; 8 ; 0.1455 ; 0.7819
14 ; 4 ; 0.0727 ; 0.8546
15 ; 8 ; 0.1455 ; 1.0001 ≅ 1 ⇒The cummulated probability thet corresponds the las value of the variable should be 1, remember probabilities take values between 0 and 1, it is 1.0001 because I rounded some decimales in the calculations. Is not important since is the forth decimal and is due to an artifice given by rounding. If the summatory of all punctual probabilities gives a number greater than 1 for more, for example if F(15)= 1.5, then you have to check your calculations, one or more of them are wrong.
Now you can calculate the asked percent, first calculate the probability:
P(X ≥ 4) = 1 - P(X < 4) ⇒ 1 - P(X ≤ 3) = 1 - 0 = 1
The study variable is defined in the range of values 4 to 15, so there is no cumulative probability for values less than 4.
100% of the respondents have at least 4 pairs of shoes.
I hope it helps!