Question

You are a coach creating a line up for your swim team. You have 4 swimmers to chose from. Would you used a permutation or a combination to determine the number of distinct orders for the next swim match

Answer 1

Combinations

Explanation:

In combinations, the order of elements does not matter, so it does in permutations. Then, it would be meaningless to have the same elements in a different order when the elements are swimmers of the same team.

For example suppose we have Paul, Alexa, Henry and Juliet as members of the swim team. Suppose also that we need to form a team of two members from the four ones above.

Permutations permit, among many others possible teams, to form two different teams. For example, the team (Paul, Alexa) and another one (Alexa, Paul); but in real life it is meaningless. The teams (Paul, Alexa) and (Alexa, Paul) are, in fact, the same ones.

In combinations, the teams (Paul, Alexa) and (Alexa, Paul) are the same ones, since the order of the elements does not matter to form different possible teams.

As a result, Combination is the choice for determining the number of distinct orders for the next swim match.

We have to remember that, mathematically, combinations are expressed as:

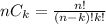`\\ nC_k = (n!)/((n-k)!k!)` [1]

And permutations as:

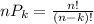`\\ nP_k = (n!)/((n-k)!)` [2]

Where n is the total number of elements and k is the number of selected elements from n, and n! is the factorial of n. For instance, 4! (4 factorial) is 4*3*2*1 = 24; 5! = 5*4*3*2*1 = 120, and so on.

It is the additional term k! in the denominator in formula [1] (compared to formula [2]) that removes the number of repetitions where the order matters, such as (Alexa, Paul) and (Paul, Alexa) and represents the difference between combinations and permutations.

As an example of the above, suppose we need to form a team of two members (k) from four members (n) (Paul, Alexa, Henry and Juliet), then, there are:

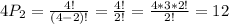`\\ 4P_2 = (4!)/((4-2)!) = (4!)/(2!) = (4*3*2!)/(2!) = 12` permutations. That is: (P, A), (P, H), (P, J), (A, P), (A, H), (A, J), (H, P), (H, A), (H, J), (J, P), (J, A), (J, H).

And
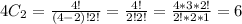`\\ 4C_2 = (4!)/((4-2)!2!) = (4!)/(2!2!) = (4*3*2!)/(2!*2*1) = 6` combinations: (P, A), (P, H), (P, J), (A, H), (A, J), (H, J).

Finally, it is crucial to notice that in the different teams there are no repetitions of an element (there is not a team of two P, for example).