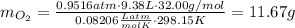Question

A mixture of hydrogen and argon gases is maintained in a 6.47 L flask at a pressure of 3.43 atm and a temperature of 85 °C. If the gas mixture contains 1.10 grams of hydrogen, the number of grams of argon in the mixture is _______ g.

B) Oxygen gas can be prepared by heating potassium chlorate according to the following equation:

2KClO3(s) ---------> 2KCl(s) + 3O2(g)

The product gas, O2, is collected over water at a temperature of 25 °C and a pressure of 747 mm Hg. If the wet O2 gas formed occupies a volume of 9.38L, the number of grams of O2 formed is _______ g. The vapor pressure of water is 23.8 mm Hg at 25 °C.

Answer 1

a. 8.37 g,

b. 11.67 g

Step-by-step explanation:

A) Given:

`V = 6.47 L`

`p = 3.43 atm`

`T = 85^oC + 273.15 K = 358.15 K`

`m_(H_2) = 1.10 g`

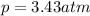
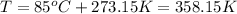
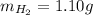
We need to find the mass of argon.

Firstly, we need to apply the ideal gas law in order to find the total number of moles of gases present in the flask:

`pV = nRT`

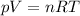
From here:

`n = (pV)/(RT)`

Substituting the variables:

`n = (3.43 atm\cdot 6.47 L)/(0.08206 (L atm)/(mol K)\cdot 358.15 K) = 0.755 mol`

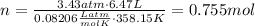
Find the number of moles of hydrogen dividing its mass by the molar mass:

`n_(H_2) = (1.10 g)/(2.016 g/mol) = 0.5456 mol`

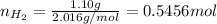
Now find the moles of argon:

`n_(Ar) = n_(total) - n_(H_2) = 0.755 mol - 0.5456 mol = 0.2094 mol`

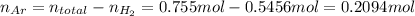
Using the molar mass of argon, convert this number into mass:

`m_(Ar) = 0.2094 mol\cdot 39.948 g/mol = 8.37 g`

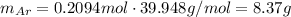
B) Given:

`T = 25^oC + 273.15 K = 298.15 K`

`p_(total) = 747 mm Hg`

`V = 9.38 L`

`p_(H_2O) = 23.8 mm Hg`

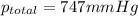
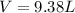
Firstly, the total pressure is equal to the sum of the vapor pressure of water and the partial pressure of oxygen. Knowing this, solve for the pressure of oxygen:

`p_(O_2) = p_(total) - p_(H_2O) = 747 mm Hg - 23.8 mm Hg = 723.2 mm Hg`

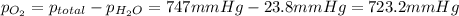
Use the ideal gas law:

`pV = nRT`

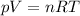
Rearrange the equation, so that we have moles in terms of the mass and the molar mass of oxygen:

`pV = (m)/(M)RT`

Convert the pressure of oxygen into atm knowing that 1 atm = 760 mm Hg. Then:

`p_(O_2) = 723.2 mm Hg\cdot (1 atm)/(760 mm Hg) = 0.9516 atm`

Now rearrange the ideal gas law equation for mass:

`m_(O_2) = (pV_(O_2)M_(O_2))/(RT)`

Solve using the variables identified:

`m_(O_2) = (0.9516 atm\cdot 9.38 L\cdot 32.00 g/mol)/(0.08206 (L atm)/(mol K)\cdot 298.15 K) = 11.67 g`