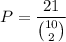Question

Six Republicans and four Democrats have applied for two open positions on a planning committee. Since all the applicants are qualified to serve, the City Council decides to pick the two new members randomly. What is the probability that both come from the same party?

Answer 1

`\displaystyle P=(7)/(15)=0.467`

Explanation:

Probabilities

When we choose from two different sets to form a new set of n elements, we use the so-called hypergeometric distribution. We'll use an easier and more simple approach by the use of logic.

We have 6 republicans and 4 democrats applying for two positions. Let's call R to a republican member and D to a democrat member. There are three possibilities to choose two people from the two sets: DD, DR, RR. Both republicans, both democrats and one of each. We are asked to compute the probability of both being from the same party, i.e. the probability is

`P=P(DD)+P(RR)`

Let's compute P(DD). Both democrats come from the 4 members available and it can be done in
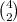`\binom{4}{2}` different ways.

For P(RR) we proceed in a similar way to get
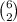`\binom{6}{2}` different ways.

The total ways to select both from the same party is

`\displaystyle \binom{4}{2}+\binom{6}{2}=4+15=21`

The selection can be done from the whole set of candidates in
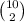`\binom{10}{2}` different ways, so

`\displaystyle P=\frac{21}{\binom{10}{2}}`

`\displaystyle P=(21)/(45)=(7)/(15)=0.467`