Question

stunt pilot weighing 0.70 kN performs a vertical circular dive of radius 0.80 km.At the bottom of the dive, the pilot has a speed of 0.20 km/s which at that instant is notchanging. What force does the plane exert on the pilot

Answer 1

To solve this problem it is necessary to apply the concepts of the Centripetal Force and the force caused by gravity. The centripetal force can be described as

`F_c = (mv^2)/(r)`

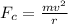
Where,

m = Mass

v = Velocity

r = Radius

At the same time the force caused by the weight can be described as

`F_g = mg \rightarrow m = (F_g)/(g)`

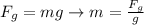
Where,

m = mass

g = Gravity

If we make a sum of Forces, the forces that act vertically on the body, both in the upward and downward direction must be equivalent to the centripetal Force, therefore

`F_f - F_g = F_c`

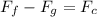
Here
`F_f` represents the force from Plane, then:

`F_f - F_g =(mv^2)/(r)`

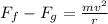
If we put the mass of the body according to the weight we would have to:

`F_f - F_g = (((F_g)/(g))v^2)/(r)`

`F_f -7kN = (((7kN)/(9.8))(0.2)^2)/(0.8)`

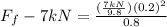
Converting to SI:

`F_f - 7000 =(((7000N)/(9.8))(200)^2)/(800)`

`F_f = 4271N`

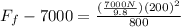
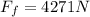
Therefore the forces that the plane exert on the pilot is 4271N