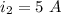Question

In an LC circuit at one time the charge stored by the capacitor is 10 mC and the current is 3.0 A. If the frequency of the circuit is (1/(4.0)) kHz, when the charge stored is 6.0 mC, what is the current?

Answer 1

`i_2=3.61\ A`

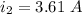
Step-by-step explanation:

LC Circuit

It's a special circuit made of three basic elements: The AC source, a capacitor, and an inductor. The charge, current, and voltage are oscillating when there is an interaction between the electric and magnetic fields of the elements. The following variables will be used for the formulas:

`q, q_1, q_2` = charge of the capacitor in any time
`t, t_1, t_2`

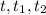
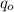`q_o` = initial charge of the capacitor

`\omega`=angular frequency of the circuit

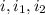`i, i_1, i_2` = current through the circuit in any time
`t, t_1, t_2`

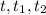
The charge in an LC circuit is given by

`q(t) = q_0 \, cos (\omega t )`

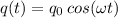
The current is the derivative of the charge

`\displaystyle i(t) = (dq(t))/(dt) = - \omega q_0 \, sin(\omega t).`

We are given

`q_1=10\ mc=0.01\ c, i_1=3\ A,\ q_2=6\ mc=0.006\ c\ ,\ f=(1000)/(4\pi)`

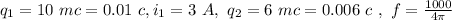
It means that

`q(t_1) = q_0 \, cos (\omega t_1 )=q_1\ .......[eq 1]`

`i(t_1) = - \omega q_0 \, sin(\omega t_1)=i_1.........[eq 2]`

From eq 1:

`\displaystyle cos (\omega t_1 )=(q_1)/(q_0)`

From eq 2:

`\displaystyle sin(\omega t_1)=-(i_1)/(\omega q_0)`

Squaring and adding the last two equations, and knowing that

`sin^2x+cos^2x=1`

`\displaystyle \left ( (q_1)/(q_0) \right )^2+\left ( (i_1)/(\omega q_0) \right )^2=1`

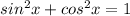
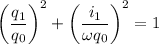
Operating

`\displaystyle \omega^2q_1^2+i_1^2=\omega^2q_o^2`

Solving for
`q_o`

`\displaystyle q_o=(√(\omega^2q_1^2+i_1^2))/(\omega)`

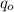
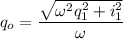
Now we know the value of
`q_0`, we repeat the procedure of eq 1 and eq 2, but now at the second time
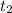`t_2`, and solve for
`i_2`

`\displaystyle \omega^2q_2^2+i_2^2=\omega^2q_o^2`

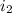
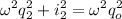
Solving for
`i_2`

`\displaystyle i_2=w√(q_o^2-q_2^2)`

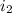
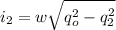
Now we replace the given values. We'll assume that the placeholder is a pi for the frequency, i.e.

`\displaystyle f=(1)/(4\pi)\ KHz`

`w=2\pi f=500\ rad/s`

`\displaystyle q_o=(√((500)^2(0.01)^2+3^2))/(500)`

`q_0=0.01166\ c`

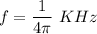
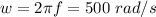
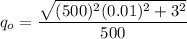
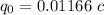
Finally

`\displaystyle i_2=500√(0.01166^2-.006^2)`

`i_2=5\ A`