Question

he mean age of bus drivers in Chicago is greater than 54.4 years. If a hypothesis test is performed, how should you interpret a decision that fails to reject the null hypothesis? There is sufficient evidence to support the claim μ > 54.4. There is sufficient evidence to reject the claim μ > 54.4. There is not sufficient evidence to support the claim μ > 54.4. There is not sufficient evidence to reject the claim μ > 54.4.

Answer 1

There is not sufficient evidence to support the claim μ > 54.4.

Explanation:

1) Previous concepts

A hypothesis is defined as "a speculation or theory based on insufficient evidence that lends itself to further testing and experimentation. With further testing, a hypothesis can usually be proven true or false".

The null hypothesis is defined as "a hypothesis that says there is no statistical significance between the two variables in the hypothesis. It is the hypothesis that the researcher is trying to disprove".

The alternative hypothesis is "just the inverse, or opposite, of the null hypothesis. It is the hypothesis that researcher is trying to prove".

2) Solution to the problem

On this case we want to test is
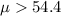`\mu>54.4` and the system of hypothesi on this case are:

Null Hypothesis:
`\mu \leq 54.4`

Alternative hypothesis:
`\mu >54.4`

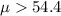
On this case is our decision is FAILS to reject the null hypothesis then we can conclude that we don't have enough evidence to support the claim at the significance level provided. So the correct conclusion would be:

There is not sufficient evidence to support the claim μ > 54.4.