Question

In a class in which the final course grade depends entirely on the average of four equally weighted 100-point tests, Charles has scored 9393, 8282, and 8787 on the first three. What range of scores on the fourth test will give Charles a C for the semester (an average between 7070 and 7979, inclusive)? Assume that all test scores have a non-negative value.

Answer 1

X must be between 1818 and 5454

Explanation:

The average A is the sum of the four notes divided by 4. We call X the value of the yet unknown fourth note, then

`A = (9393+8282+8787+X)/(4)`

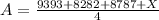
If you want A to be between 7070 and 7979, then we need X such that

`[tex]7070 \leq  (9393+8282+8787+X)/(4) \leq 7979 \, \rightarrow 28280 \leq 9393+8282+8787+X< 31916 \\\rightarrow 28280-9393-8282-8787 \leq X \leq 31916 - 9393-8282-8787 \, \rightarrow 1818 \leq X \leq 5454`

Therefore, X must be between 1818 and 5454.