Answer:
see explanation
Explanation:
The perimeter is the sum of the 3 sides, that is
perimeter = 8 + 12 + 17 = 37 cm
To use Heron's formula for area (A)
A =
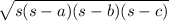
where a, b and c are the lengths of sides and s the semi perimeter
s = 37 ÷ 2 = 18.5
let a = 8, b = 12 and c = 17, then
A =
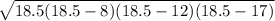
=
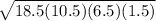
=
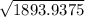 ≈ 43.52 cm² ( to 2 dec. places )
≈ 43.52 cm² ( to 2 dec. places )