Question

A ball is shot straight up from the top of a 15-story building. The motion of the ball could be described by the function: h(t)= -16t^2 + 144t + 160 where t represents the time the ball is in the air in seconds and h(t) represents the height in feet .What is the height of the ball after 4 seconds?What is the maximum height of the ball?At what time will the ball hit the ground?

Answer 1

• After 4 seconds the height is 480 meters.
• The maximum height is 484 meters.
• The ball hits the ground after 10 seconds

Explanation:

The height after four seconds is h(4) = -16 * r² + 144*4+160 = 480

The maximum height of the ball is the value it takes at its vertex 'v = -b/2a'. In this case a = -16 and b = 144, so the v = -144/-32 = 4.5. The maximum height of the ball as a result is h(4.5) = -16 (4.5)² + 144*4.5 + 160 = 484

To find the moment the ball hits the ground, we need to find when h takes the value 0 by using the quadratic formula, with a = -16, b = 144 and c = 160.

`r_1,r_2 = (-144 \, ^+_- √(144^2-4*(-16)*160))/(2*(-16)) = (-144 \, ^+_- √(30976))/(-32) = (-144 \, ^+_- 176)/(-32) = -1, 10`

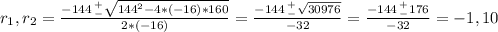
Since t cant take negative values, then the correct value is 10. The ball hits the ground after 10 seconds.