Answer:
The initial velocity of the projectile is 50 meters per minute
Step-by-step explanation:
The equation that describes the height (h on meters) of the projectile as a function of time (t in minutes) is:
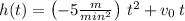 (1)
(1)
We already know at 10 minutes the projectile reaches the ground, so if we assume our coordinate system on the ground that implies h(10 min)=0m, using this on (1):

solving for
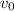 :
:
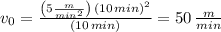
Note: It’s important to have a careful use of units in this kind of problem to avoid errors in the units of our answers, if we are calculating velocity we should get velocity units.