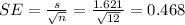Question

s a t-Distribution Appropriate? A sample with size has and . The dotplot for this sample is given below. A dotplot ranging from 5 to 11 with dots plotted as follows: 1 dot above 5, 2 dots above 6, 3 dots above 7, 3 dots above 8, 2 dots above 9, and 1 dot above 11. Indicate whether or not it is appropriate to use the t-distribution.

Answer 1

For this case since the sample size is < 30 is appropiate use the t distribution.

`df=n-1=12-1=11`

`SE= (s)/(√(n))=(1.621)/(√(12))=0.468`

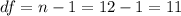
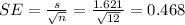
Explanation:

The t distribution (Student’s t-distribution) is a "probability distribution that is used to estimate population parameters when the sample size is small (n<30) or when the population variance is unknown".

The shape of the t distribution is determined by its degrees of freedom and when the degrees of freedom increase the t distirbution becomes a normal distribution approximately.

The degrees of freedom represent "the number of independent observations in a set of data. For example if we estimate a mean score from a single sample, the number of independent observations would be equal to the sample size minus one."

Based on the info given we have these values:

5, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 11

And for this case we have n=12 representing the sample size.

For this case since the sample size is < 30 is appropiate use the t distribution.

We can calculate the sample mean and the deviation with the following formulas:

`\bar X =(\sum_(i=1)^n X_i)/(n)=7.583`

`s=(\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)=1.621`

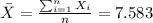
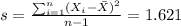
We can calculate the degrees of freedom like this:

`df=n-1=12-1=11`

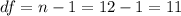
And the standard error for the sample mean is given by:

`SE= (s)/(√(n))=(1.621)/(√(12))=0.468`