Question

The point A (5,11) is reflected across the x-axis. How long is the segment AA'?
​

Answer 1

The reflected point of A (5,11) across the x-axis is A' (5,-11). Using the distance formula derived from the Pythagorean theorem, the length of segment AA' is calculated to be 22 units.

Step-by-step explanation:

When reflecting a point across the x-axis, the x-coordinate remains the same, but the y-coordinate changes sign. For the point A (5,11), its reflected point A' would be (5,-11). To find the length of the segment AA', we can use the distance formula, which is derived from the Pythagorean theorem.

The distance formula is √((x2 - x1)² + (y2 - y1)²), where (x1, y1) and (x2, y2) are the coordinates of the two points. Applying this to our points A and A', the distance is √((5 - 5)² + (-11 - 11)²) = √(0 + (-22)²) = √484 = 22 units.

Therefore, the length of segment AA' is 22 units.

Answer 2

Answer: The required length of the segment AA' is 11 units.

Step-by-step explanation: Given that the point A(5, 11) is reflected across the X-axis.

We are to find the length of the segment AA'.

We know that

if a point (x, y) is reflected across X-axis, then its co-ordinates becomes (x, -y).

So, after reflection, the co-ordinates of the point A(5, 11) becomes A'(5, -11).

Now, we have the following distance formula :

The DISTANCE between two points P(a, b) and Q(c, d) gives the length of the segment PQ as follows :

`PQ=√((c-a)^2+(d-b)^2).`

Therefore, the length of the segment AA' is given by

`AA'=√((5-5)^2+(-11-11)^2)=√(11^2)=11.`

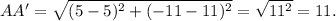
Thus, the required length of the segment AA' is 11 units.