Answer:
Net acceleration,
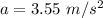
Step-by-step explanation:
It is given that,
mass of the person, m = 56 kg
Inclination with the horizontal,
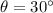
The coefficient of friction between the skis and the snow is 0.16
Let
 is the acceleration due to gravity on the object,
is the acceleration due to gravity on the object,
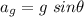
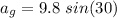
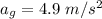
Let
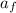 is the acceleration of the normal reaction. It is given by:
is the acceleration of the normal reaction. It is given by:
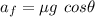
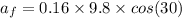

Let a is the net acceleration of the person. It is equal to,
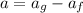
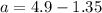
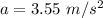
So, the magnitude of net acceleration is
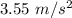 . Hence, this is the required solution.
. Hence, this is the required solution.