Question

Pilots can be tested for the stresses of flying high-speed jets in a whirling "human centrifuge," which takes 1.5 min to turn through 21 complete revolutions before reaching its final speed.

A) What was its angular acceleration (assumed constant)?
B) What was its final angular speed in rpm?

Answer 1

(a) 0.0326 rad/s²

(b) 2.93 rad/s

Step-by-step explanation:

number of revolutions, n = 21

time taken , t = 1.5 minutes = 90 seconds

Angle turned, θ = 2 x π x n = 2 x 3.14 x 21 = 131.88 rad

Let α be the angular acceleration.

initial angular velocity, ωo = 0 rad/s

Use second equation of motion

`\theta =\omega _(0)t+(1)/(2)\alpha t^(2)`

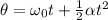
131.88 = 0 + 0.5 x α x 90 x 90

α = 0.0326 rad/s²

(b) Let the final angular speed is ω

Use first equation of motion

ω = ωo + αt

ω = 0 + 0.0326 x 90 = 2.93 rad/s

Answer 2

(a) Angular acceleration will be
`\alpha =18.66rev/min^2`

(B) Final angular velocity will be 28 rev/min

Step-by-step explanation:

We have given time t = 1.5 min

Angular displacement
`\Theta =21rev`

(a) Initial angular speed
`\omega _i=0rad/sec`

From second equation of motion we know that
`\Theta =\omega _it+(1)/(2)\alpha t^2`

So
`21 =0* 1.5+(1)/(2)* \alpha*  1.5^2`

`42 =\alpha*  1.5^2`

`\alpha =18.66rev/min^2`

(b) Now from first equation of motion

`\omega _f=\omega _i+\alpha t=0+18.66* 1.5=28rev/min`