Question

A 10 kg projectile is fired from a cannon at an angle of 60^ above the horizontal and with an initial velocity of 300 m/s.At the highest point of its flight,the projectile explodes into two fragments with equal mass.One of the fragments falls vertically downwards with an initial velocity of zero.

Question 1: How far from the cannon does the other fragment strike the ground( assume the ground is level)?

Question 2: How much energy is released during the explosion?

Answer 1

The distance the other fragment strikes the ground can be found using projectile motion principles, considering conservation of momentum. The energy released during the explosion can be calculated by considering the conservation of energy and the kinetic energy of the fragments post-explosion.

Step-by-step explanation:

Projectile Motion and Energy Conservation

A 10 kg projectile is fired from a cannon at a 60-degree angle above the horizontal with an initial velocity of 300 m/s. At the peak of its trajectory, the projectile explodes into two fragments of equal mass. When one fragment falls vertically, we can analyze the motion of the other fragment using the conservation of momentum and projectile motion principles. The explosion does not change the horizontal component of velocity for the system, so we use this to find the distance it strikes from the cannon.

To answer question 1: Since the horizontal component of velocity doesn't change due to the explosion, the fragment that keeps moving horizontally will continue with the initial horizontal speed of the projectile, which is calculated as initial velocity × cosine(angle). The total horizontal range can be found by using the time of flight for the entire projectile, determined by the vertical movement. This time is double the time it takes to reach the highest point, which can be calculated using the initial vertical speed (initial speed × sin(angle)) and the acceleration due to gravity.

To answer question 2: The energy released during the explosion can be calculated by considering the conservation of energy. Initially, the projectile has both kinetic and potential energy; however, after the explosion, one fragment falls with zero kinetic energy. This increase in gravitational potential energy of the stationary fragment is equal to the kinetic energy of the moving fragment plus the energy released in the explosion.

Answer 2

Question 1, answer = 7950[m]. Question 2, answer = 394250 [J]

Step-by-step explanation:

There are certain conditions of this problem, which can simplify its solution, the first condition is that when the ball reaches the highest point its velocity in the y- axis component and is zero, in this way we can use the following kinematic equation for parabolic motion.

But first let's decompose the initial velocity into x & y

`(v_(x))_(0) = 300*cos(60) = 150[m/s}\\ (v_(y))_(0) =300*sin(60) = 260 [m/s]\\`

`v_(y) =(v_(y) )_(0) -a*t \\where:\\a= gravity = 9.81[m/s^2]\\t=time [s]\\v_(y) = 0`

Now replacing the values:

`0=260- (9.81)*t\\t= 26.48[s]`

With this time and the next equation, we can find the highest point of the trajectory

`y=(v_(y) )_(0)*t - (1)/(2) *a*t^(2) \\replacing\\y= (260*26.48) - (1)/(2) *(9.81)*(26.48)^(2) \\\\y=3446 [m]`

Now we have the highest point, so we can find the potential energy, which will be useful for solving question 2.

For solving question 1, we need to find the time when one of the fragments is on the ground, therefore.

`y=(v_(y) )_(0) *t - (1)/(2) *a*t^(2) \\where\\y=0\\(v_(y) )_(0) =260[m/s]\\replacing\\0=(260*t)-4.91*t^(2) \\4.91t^(2)=260t\\ t=53[s]`

Now using this time for the movement in the x-axis.

`x = (v_(x) )_(0) *t\\where\\t=53[s]\\(v_(x) )_(0)=150[m/s]\\replacing\\x=150*53 = 7950 [m]`

The total amount of energy due explosion will be equal to the sum of the energies at that precise moment.

`E_(exp) =E_(p1)+ E_(p2)+E_(k1)+E_(k2)`

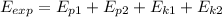
The above equation tells us that the energy of the explosion is equal to the sum of the potential and kinetic energies of both fragments.

Let us remember that both fragments are of equal mass.

Fragment 1

`m_(1)=5 [kg]\\ Ep_(1)= m_(1)*g*y\\where:\\g=gravity=9.81[m/s}\\y=3446 [m]\\ Ep_(1)=5*9.81*3446\\Ep_(1)=169026.3[J] = 169 [kJ]`

The kinetic energy for the fragment 1 is zero, because it falls downwards with an initial velocity of zero.

Fragment 2

`m_(2)=5[kg]\\E_(p2)= m_(2)*g*y\\E_(p2)=5*9.81*3446\\E_(p2)=169[kJ]`

Now for the kinetic energy we will use the velocity calculated v = 150 [m/s], this is the velocity of the fragment 2 in the x-axis.

`E_(k2)=(1)/(2) *m*v_(2) ^(2)  \\E_(k2)=(1)/(2)*5*(150)^(2)\\  E_(k2)= 56250[J]\\ E_(k2)=56.25[kJ]`

`E_(exp) = 169+56.25+169+0\\E_(exp) =394.25[kJ] = 394250[J]`