Answer:
a)
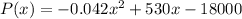
b)
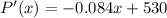
c)
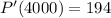
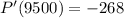
Explanation:
a)
We know that Revenue is our total income and cost is our total cost. Thus, profit is what's left after cost is subtracted from Income (revenue). Thus, we can say:
P(x) = R(x) - C(x)
Finding Profit Function (P(x)):
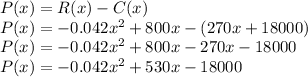
This is the profit function.
b)
The marginal profit is the profit earned when ONE ADDITIONAL UNIT of the product is sold. This is basically the rate of change of profit per unit. We find this by finding the DERIVATIVE of the Profit Function.
Remember the power rule for differentiation shown below:
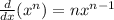
Now, we differentiate the profit function to get the marginal profit function (P'):

This is the marginal profit function , P'.
c)
We need to find P'(4000) and P'(9500). So we basically put "4000" and "9500" in the marginal profit function's "x". The value is shown below:
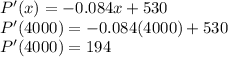
and
