Question

Which of the following geometric series is a representation of the repeating decimal 0.999999…?

Answer 1

A & C.

.99+.0099+.000099

&

.9+.09+.009

Explanation:

Answer 2

9(1/10) [1+(1/10)+(1/10)^2+(1/10)^3+.....]

Explanation:

0.99999...= 9(1/10) + 9(1/10)^2+9(1/10)^3+9(1/10)^4+.....

taking 9(1/10) common,

=9(1/10) [1+(1/10)+(1/10)^2+(1/10)^3+.....]

therefore, this is the required geometric series.

• the sum of the infinite series: 1+r+r^2+r^3+r^4+r^5+r^6....

is,
`(1)/(1-r)`

• the series inside the square brackets are infinite geometric progression series.

so the whole sum = 9(1/10)[
`(1)/(1-(1)/(10) )`]

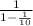=9(1/10)[10/9]

=1