Answer:
1. (b)
2. (b)
Explanation:
1.
We have,
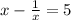
Now, squaring both sides, we get
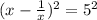 .......(1)
.......(1)
Now, using the identity
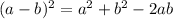 in the LHS of the equation (1), we get
in the LHS of the equation (1), we get
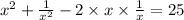
⇒

⇒
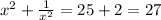
∴ The correct answer is option (b).
2.
We have,
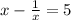
Now, squaring both sides, we get
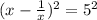 .......(1)
.......(1)
Now, using the identity
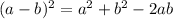 in the LHS of the equation (1), we get
in the LHS of the equation (1), we get
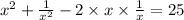
⇒

⇒
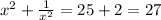 .......(2)
.......(2)
Again, squaring both sides of equation (2), we get
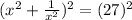 .......(3)
.......(3)
Now, using the identity
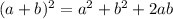 in the LHS of the
in the LHS of the
equation (3), we get
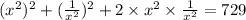
⇒
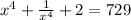
⇒
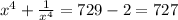
∴ The correct answer is option (b).