Question

The mean diameters of Mars and Earth are 6.9 ✕ 103 km and 1.3 ✕ 104 km, respectively. The mass of Mars is 0.11 times Earth's mass.

(a) What is the ratio of the mean density of Mars to that of Earth?
(b) What is the value of g on Mars? m/s2
(c) What is the escape speed on Mars? m/s2

Answer 1

(a) 0.72

(b) 3.83 m/s^2

(c) 5.1 Km/s

Step-by-step explanation:

diameter of Mars = 6.9 x 10^3 km

Radius of Mars, Rm = 3.45 x 10^3 km = 3.45 x 10^6 m

diameter of earth = 1.3 x 10^4 km

radius of earth, Re = 6.5 x 10^3 km = 6.5 x 10^6 m

Let Me be the mass of earth.

Mass of Mars, Mm = 0.11 Me

(a) Volume of Mars, Vm = 4/3 x 3.14 x (3.45 x 10^6)³ = 1.72 x 10^20 m³

Volume of earth, Ve = 4/3 x 3.14 x (6.5 x 10^6)³ = 1.15 x 10^21 m³

density is the ratio of mass to the volume of the object.

`(d_(m))/(d_(e))=(M_(m))/(M_(e))* (V_(e))/(V_(m))`

`(d_(m))/(d_(e))=(0.11M_(e))/(M_(e))* (1.15*10^(21))/(1.72*10^(20))`

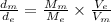
density of mars : density of earth = 0.72

(b) The value of acceleration due to gravity

`g=(GM)/(R^(2))`

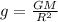
Let gm be the acceleration due to gravity on Mars

`(g_(m))/(g_(e))=(M_(m))/(M_(e))* (R_(e)^(2))/(R_(m)^(2))`

`(g_(m))/(g_(e))=(0.11M_(e))/(M_(e))* (6.5*6.5)/(3.45*3.45)`

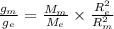
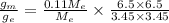
gm = 3.83 m/s^2

(c) The escape velocity is given by

`v=√(2gR)`

`(v_(m))/(v_(e))=\sqrt{(g_(m)* R_(m))/(g_(e)* R_(e))}`

`(v_(m))/(v_(e))=\sqrt{(3.83* 3.45)/(9.8* 6.5)}`

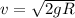
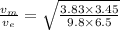
escape velocity for mars = 5.1 Km/s

Answer 2

(a) Ratio of mean density is 0.735

(b) Value of g on mars 0.920
`m,/sec^2`

(c) Escape velocity on earth is
`3.563* 10^4m/sec`

Step-by-step explanation:

We have given radius of mars
`R_(mars)=6.9* 10^3km=6.9* 10^6m` and radius of earth
`R_(E)=1.3* 10^4km=1.3* 10^7m`

Mass of earth
`M_E=5.972* 10^(24)kg`

So mass of mars
`M_m=5.972** 0.11 * 10^(24)=0.657* 10^(24)kg`

Volume of mars
`V=(4)/(3)\pi R^3=(4)/(3)* 3.14* (6.9* 10^6)^3=1375.357* 10^(18)m^3`

So density of mars
`d_(mars)=(mass)/(volume)=(0.657* 10^(24))/(1375.357* 10^(18))=477.69kg/m^3`

Volume of earth
`V=(4)/(3)\pi R^3=(4)/(3)* 3.14* (1.3* 10^7)^3=9.198* 10^(21)m^3`

So density of earth
`d_(E)=(mass)/(volume)=(5.972* 10^(24))/(9.198* 10^(21))=649.271kg/m^3`

(A) So the ratio of mean density
`(d_(mars))/(d_E)=(477.69)/(649.27)=0.735`

(B) Value of g on mars

g is given by
`g=(GM)/(R^2)=(6.67* 10^(-11)*0.657* 10^(24))/((6.9* 10^6)^2)=0.920m/sec^2`

(c) Escape velocity is given by

`v=\sqrt{(2GM)/(R)}=\sqrt{(2* 6.67* 10^(-11)* 0.657* 10^(24))/(6.9* 10^6)}=3.563* 10^4m/sec`