Answer:
There is statistical evidence to support that the sample proportion is only 0.50.
Explanation:
given that a random sample of 50 university admissions officers was asked about expectations in application interviews.
Sample proportion =
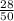
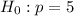
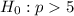
(Right tailed test at 5% significance level)
p difference = 0.06
Assuming H0 to be true p will have normal distribution with
std error =
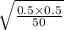
Test statistic = p difference/std error
=
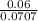
=0.8485
p value = 0.19808
Since p is greater than alpha, we accept null hypothesis
There is statistical evidence to support that the sample proportion is only 0.50.