Question

Josh starts his sled at the top of a 3.1 m-high hill that has a constant slope of 25 degrees. After reaching the bottom, he slides across a horizontal patch of snow. The hill is frictionless, but the coefficient of kinetic friction between his sled and the snow is 0.08. How far from the base of the hill does he end up?

Answer 1

38.8 m

Explanation:

Height of hill, h = 3.1 m

slope of hill, θ = 25°

coefficient of friction, μ = 0.08

Let v be the velocity of Josh as he reaches at the bottom of hill.

By use of conservation of energy

m x g x h = 0.5 x m x v²

9.8 x 3.1 = 0.5 x v²

v = 7.8 m/s

Now Josh is moving on the snow with initial velocity, u = 7.8 m/s

final velocity is zero. Let he travels upto a distance of s.

Use third equation of motion

v² = u² + 2as

0 = 7.8² - 2 x 0.08 x 9.8 x s

s = 38.8 m

Thus, the distance traveled by Josh before stopping is 38.8 m.

Answer 2

stopping distance = 38.75 m

Explanation:

Given data:

height of sliding hill = 3.1 m

slope =25 degree

coefficient of friction is 0.08

Gravitational energy is given as E

E = Mgh

E = 3.1 Mg joule

As the hill is frictionless, thus all energy is converted to kinectic energy

Total work done to stop the sliding is

work done = force × distance

we know that

coefficient of friction is given as

`\mu = (F_f)/(F_n)`

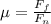
where F_f - friction force

F_n - normal friction force

`F_f = 0.08 * Mg`

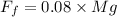
so wrok done
`= 0.08 Mg * stopping/ distance`

`3.1 Mg = 0.08 Mg * stopping / distance`

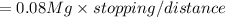
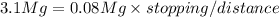
so

stopping distance = 38.75 m