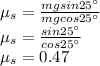Question

A 100-kg box is placed on a ramp. As one end of the ramp is raised, the box begins to move downward just as the angle of inclination reaches 25°. What is the coefficient of static friction between box and ramp?

Answer 1

`\mu_s=0.47`

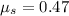
Step-by-step explanation:

Just before the box starts moving, according to Newton's first law, we have:

`\sum F_x:F_f-W_x=0(1)\\\sum F_y:N-W_y=0(2)`

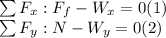
The sine of the angle (25°) of a right triangle is defined as the opposite cathetus (
`W_x`) to that angle divided into the hypotenuse (W):

`sin25^\circ=(W_x)/(W)\\W_x=Wsin25^\circ\\W_x=mgsin25^\circ(3)`

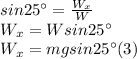
The cosine of the angle (25°) of a right triangle is defined as the adjacent cathetus (
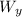`W_y`) to that angle divided into the hypotenuse (W):

`cos25^\circ=(W_y)/(W)\\W_y=Wcos25^\circ\\W_y=mgcos25^\circ(4)`

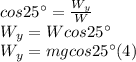
Recall that the maximum frictional force is defined as:

`F_f=\mu_s N(5)`

Replacing (3) in (1) and (4) in (2):

`F_f=mgsin25^\circ(6)\\N=mgcos25^\circ(7)`

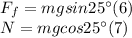
Replacing (7) and (6) in (5) and solvinf for
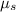`\mu_s`:

`\mu_s=(mgsin25^\circ)/(mgcos25^\circ)\\\mu_s=(sin25^\circ)/(cos25^\circ)\\\mu_s=0.47`