Answer
given,
mass of car (m) = 1200 Kg
speed of cur, u = 25 m/s
mass of truck(M) = 9000 Kg
speed of truck, u' = 20 m/s
v = 18 m/s
a) using conservation of momentum
m u + M u' = m v + M v'
1200 x 25 + 9000 x 20 = 1200 x 18 + 9000 x v'
9000 v' = 188400
v' = 20.93 m/s
b) To calculate losses, we will find the kinetic energies before & after collision. Any difference would give us the losses (in energy form).
(K E)₁= (K E)₂+ Losses
losses = (K E)₂ - (K E)₁
=

=
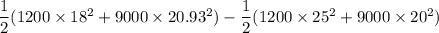
=9038 J