Question

A ball of mass m = 4.6 kg, at one end of a string of length L= 6.6 m, rotates in a vertical circle just fast enough to prevent the string from going slack at the top of the circle. Assuming mechanical energy is conserved, calculate the speed of the ball at the bottom of the circle.

Answer 1

v₂ = 17.98 m/s

Step-by-step explanation:

given,

mass of ball = m = 4.6 Kg

length of string = L = 6.6 m

force acting toward the center is equal to the force exerted by centripetal acceleration

`m g = (mv_1^2)/(r)`

`v_1 = √(gr)`

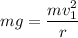
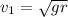
now, calculating the speed of ball at the bottom of the circlr

work done by the gravity = change in kinetic energy

`- m g (2R) = (1)/(2)m(v_1^2-v_2^2)`

`-4 gR =v_1^2-v_2^2`

`-4 gR =g R-v_2^2`

`v_2^2 = 5 g R`

`v_2=√(5* 9.8 * 6.6)`

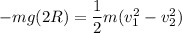
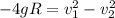
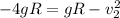
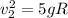
v₂ = 17.98 m/s