Question

A 73-kg boy is surfing and catches a wave which gives him an initial speed of 1.6 m/s. He then drops through a height of 1.60 m, and ends with a speed of 8.5 m/s. How much non-conservative work was done on the boy?

Answer 1

To solve this problem it is necessary to apply the concepts related to the Conservation of Energy, for which it is necessary that any decrease made through the potential energy, is equivalent to the gain given in the kinetic energy or vice versa.

Mathematically this can be expressed as

`KE_i+PE_i = KE_f+PE_f`

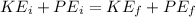
Since there is no final potential energy (the height is zero), and the initial potential energy is equivalent to the work done we have to

`W = KE_f-KE_i-PE_i`

`W = (1)/(2)mv_f^2-(1)/(2)mv_i^2 -mgh`

`W =(1)/(2) m(v_f^2-v_i^2)-mgh`

`W= (1)/(2)(73)(8.5^2-1.6^2)-(73*9.8*1.6)`

`W= 1399.045J`

`W= 1.4kJ`

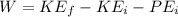
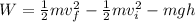
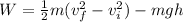
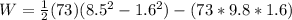
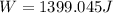
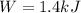
Therefore the non-conservative work was done on the boy is 1.4kJ