Question

A bicycle wheel of radius 14 cm is mounted at the middle of an axle 96 cm long. The tire and rim weigh 23 N. The wheel is spun at 12 rev/s, and the axle is then placed in a horizonal position with one end resting on a pivot

a. What is the magnitude of the angular momentum due to the spinning of the wheel? (Treat the wheel as a hoop.)
b. What is the angular speed of precession? rad/s How long does it take for the axle to swing through 360 degree around the pivot?
c. What is the magnitude of the angular momentum associated with the motion of the center of mass, that is, due to the d. precession? In what direction is this angular momentum? up up or down, depending on the direction of in part (a) down

Answer 1

a. L =3.465 J.s

b. 3.186 rad/s

c. T = 1.972 s

d. Lp = 0.022 J.s; up or down, depending on the direction of L

Step-by-step explanation:

(a)We have the formula for angular momentum as

L = I*w where I = moment of inertia =
`M*R^2`

L =
`(23/9.81) * 0.14^2* (24*pi) J.s = 3.465 J.s`

(b) ω = M*g*D/L

where D = L/2 = 0.96/2 = 0.48m

ω = (23* 0.48/3.465) rad/s = 3.186 rad/s

(c) T = 2π/ω

T = 2*π/3.186 s = 1.972 s

(d) Lp =
`M*D^(2*w)`

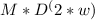
Solving with mass M, D and angular velocity ω

Lp = 0.022 J.s; up or down, depending on the direction of L