Question

A 51.24-g sample of Ba(OH)2 is dissolved in enough water to make 1.20 liters of solution. How many mL of this solution must be diluted with water in order to make 1.00 liter of 0.100 molar Ba(OH)2 ?

Answer 1

0.40 L

Step-by-step explanation:

Calculation of the moles of
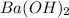`Ba(OH)_2` as:-

Mass = 51.24 g

Molar mass of
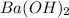`Ba(OH)_2` = 171.34 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

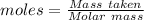
Thus,

`Moles= (51.24\ g)/(171.34\ g/mol)`

`Moles= 0.2991\ mol`

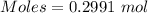
Volume = 1.20 L

The expression for the molarity is:

`Molarity=(Moles\ of\ solute)/(Volume\ of\ the\ solution)`

`Molarity=(0.2991\ mol)/(1.20\ L)=0.24925\ M`

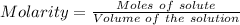
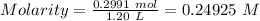
Thus,

Considering

`Molarity_(working\ solution)* Volume_(working\ solution)=Molarity_(stock\ solution)* Volume_(stock\ solution)`

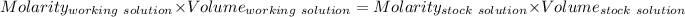
Given that:

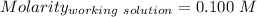
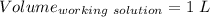
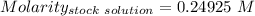
`Molarity_(working\ solution)=0.100\ M`

`Volume_(working\ solution)=1\ L`

`Volume_(stock\ solution)=?`

`Molarity_(stock\ solution)=0.24925\ M`

So,

`0.100\ M* 1\ L=0.24925\ M* Volume_(stock\ solution)`

`Volume_(stock\ solution)=(0.100* 1)/(0.24925)\ L=0.40\ L`

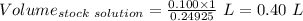
The volume of 0.24925M stock solution added = 0.40 L