Answer:
600 N
119366.20731 Pa
Step-by-step explanation:
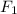 = Force on the smaller piston
= Force on the smaller piston
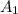 = Area of the smaller piston =
= Area of the smaller piston =
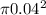
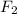 = Force on the larger piston = 15000 N
= Force on the larger piston = 15000 N
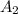 = Area of the larger piston =
= Area of the larger piston =
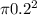
From Pascal's law we have
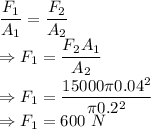
The force that must be applied to the small piston is 600 N
Pressure would be
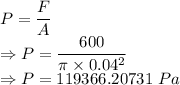
The pressure applied to the fluid in the lift is 119366.20731 Pa