Question

A gymnast is swinging on a high bar. The distance between his waist and the bar is 0.829 m, as the drawing shows. At the top of the swing his speed is momentarily zero. Ignoring friction and treating the gymnast as if all of his mass is located at his waist, find his speed at the bottom of the swing.

Answer 1

To find the speed with the given values we can apply the energy conservation equations for which we have that the increase in potential energy is compensated in the decrease of the kinetic energy or vice versa.

Since there is conservation and part of the balance we have to

`KE = PE`

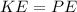
Where,

KE = Kinetic Energy

PE = Potential Energy

The values for this energy are given as

`(1)/(2)mv^2 = mgh`

`(1)/(2) v^2 = gh`

`v = √(2gh)`

`v = √(2(9.8)(0.829))`

`v = 4.03m/s`

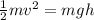
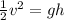
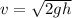
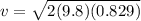
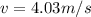
Therefore the speed at the bottom of the swing is 4.03m/s