Question

A couple of astronauts agree to rendezvous in space after hours. Their plan is to let gravity bring them together. She has a mass of 60.0 kg and he a mass of 74.0 kg , and they start from rest 23.0 m apart.(a) Make a free-body diagram of each astronaut, and use it to find his or her initial acceleration. As a rough approximation, we can model the astronauts as uniform spheres. (b) If the astronauts’ acceleration remained constant, how many days would they have to wait before reaching each other? (Careful! They both have acceleration toward each other.) (c) Would their acceleration, in fact, remain constant? If not, would it increase or decrease? Why?

Answer 1

(a) Acceleration of female astronaut = 9.33*10^-12 m/s^2; Acceleration of male astronaut = 7.56*10^-12 m/s^2

(b) 27.013 days

(c) No, their accelerations would not be constant.

Step-by-step explanation:

In the given question, we have:

Mass of female astronaut
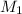`M_(1)` = 60.0 kg

Mass of male astronaut
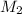`M_(2)` = 74.0 kg

Distance between them (S) = 23.0 m

(a) The free-body diagram is shown in the attached figure.

Using the equations below, the initial accelerations of the two astronauts can be calculated:

Force of gravity (F) =
`(G*M_(1)*M_(2))/(S^(2) )`

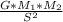
G = 6.67*10^-11
`(m^(3) )/(kg*s^(2) )`

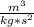
F = (6.67*10^-11 *60*74)/23^2 = 5.598*10^-10 N

For the female astronaut, her initial acceleration = F/
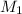`M_(1)` = 5.598*10^-10/60 = 9.33*10^-12 m/s^2

For the male astronaut, his acceleration = F/
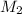`M_(2)` = 5.598*10^-10/74 = 7.56*10^-12 m/s^2

(b) Since the different between their mass is not much, we can deduce that:

`a_(average) = (a_(1)+a_(2))/(2)` = (9.33*10^-12 + 7.56*10^-12)/2 = 8.445*10^-12 m/s^2

Using the equation below, we can calculate the the time:

S = ut + 1/2 (at^2) where u = 0

23 = 1/2 (8.445*10^-12)*t^2

t^2 = 5.447*10^12

t = 2333883.044 s = 27.013 days

(c) No, their accelerations will not be constant. It will increase because their radii would be decreasing.