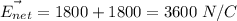A long, thin rod parallel to the y-axis is located at x = - 1 cm and carries a uniform positive charge density λ = 1 nC/m . A second long, thin rod parallel to the z-axis is loc…

Question

asked Nov 21, 2020 101k views

1 Answer

Jamesls · Answer 1 · 2020-11-26T08:47:35+0000

Answer:

The electric field at origin is 3600 N/C

Solution:

As per the question:

Charge density of rod 1,
$\lambda = 1\ nC = 1* 10^(- 9)\ C$

Charge density of rod 2,
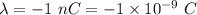
$\lambda = - 1\ nC = - 1* 10^(- 9)\ C$

Now,

To calculate the electric field at origin:

We know that the electric field due to a long rod is given by:

$\vec{E} = \frac{\lambda }{2\pi \epsilon_(o){R}$

Also,

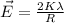$\vec{E} = (2K\lambda )/(R)$ (1)

where

K = electrostatic constant =
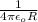
$(1)/(4\pi \epsilon_(o) R)$

R = Distance

$\lambda$ = linear charge density

Now,

In case, the charge is positive, the electric field is away from the rod and towards it if the charge is negative.

At x = - 1 cm = - 0.01 m:

Using eqn (1):

$\vec{E} = (2* 9* 10^(9)* 1* 10^(- 9))/(0.01) = 1800\ N/C$

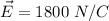$\vec{E} = 1800\ N/C$ (towards)

Now, at x = 1 cm = 0.01 m :

Using eqn (1):

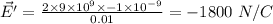
$\vec{E'} = (2* 9* 10^(9)* - 1* 10^(- 9))/(0.01) = - 1800\ N/C$

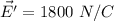$\vec{E'} = 1800\ N/C$ (towards)

Now, the total field at the origin is the sum of both the fields:

$\vec{E_(net)} = 1800 + 1800 = 3600\ N/C$