Answer:
a) Length = 2.30 ft
b) Width = 2.30 ft
c) Height = 3.781 ft
Explanation:
First we need to understand the information given:
- There's a rectangular box (cuboid) with a square base and top, and sides
the volume of a cuboid is :
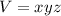 , but in our case, the base is a square so,
, but in our case, the base is a square so,
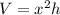 (i prefer h because its denoting the height of the cuboid, you can choose any variable)
(i prefer h because its denoting the height of the cuboid, you can choose any variable)
As, the volume is already given as
 , we can write:
, we can write:
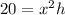
- the cost of each side's area is different.
Let's put this much info into an equation for cost (C)
C = cost of top + cost of bottom + costs of sides.
each cost given in the question is in
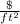 , so then we should be interested in the areas of each face of the cuboid.
, so then we should be interested in the areas of each face of the cuboid.
Areas:
Area of top and bottom will be the same since they are squares.
Area of top =

Area of bottom =

Area of sides =
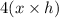 , there are 4 sides remaining after excluding the top and bottom and they all have the same area.
, there are 4 sides remaining after excluding the top and bottom and they all have the same area.
The cost of each side will be:
Cost of top =
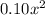
Cost of bottom =
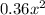
Cost of sides =
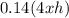
Now coming back to the equation for our cost.
C = cost of top + cost of bottom + costs of sides.

here, we can see that C is a function of both x and h, so for the purposes of notation we can also write:

what we need to do now, is to find the minimum cost from this equation. That can be done either through differentiation or plotting.
but before that, we need to make this equation in terms of only one variable!
so, to get rid of 'h' in the equation we will need the equation of the Volume that we derived earlier.
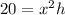

and substitute into our cost equation:
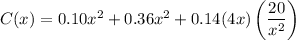
simplify:
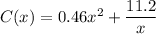 = this is the equation of cost
= this is the equation of cost
- we need to first differentiate C with respect to x, and to find the minimum value we'll equate that equation to zero.
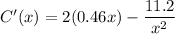
finding the minimum value.

solve for x:
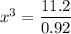
![x = \sqrt[3]{(11.2)/(0.92)}](https://img.qammunity.org/2020/formulas/mathematics/college/u1saruj3s0sc8nfqznueqooyhudj020wav.png)
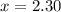
this is the length of the sides of the square base of the rectangular box.
and to find the height of the box

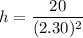
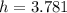
The Answer is:
a) Length =
 =2.30 ft
=2.30 ft
b) Width =
 = 2.30 ft
= 2.30 ft
c) Height =
 = 3.781 ft
= 3.781 ft