Question

A mass of 5kg starts from rest and pulls down vertically on a string wound around a disk-shaped, massive pulley. The mass of the disk is 5kg and its radius is 2 m. What is the linear speed, in m/s, after the mass drops by 0.3 m?

a. 0.5
b. 1.5
c. 2
d. 3
e.5

Answer 1

c. V = 2 m/s

Step-by-step explanation:

Using the conservation of energy:

`E_i =E_f`

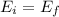
so:

Mgh =
`(1)/(2)IW^2 +(1)/(2)MV^2`

where M is the mass, g the gravity, h the altitude, I the moment of inertia of the pulley, W the angular velocity of the pulley and V the velocity of the mass.

Also we know that:

V = WR

Where R is the radius of the disk, so:

W = V/R

Also, the moment of inertia of the disk is equal to:

I =
`(1)/(2)MR^2`

I =
`(1)/(2)(5kg)(2m)^2`

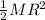
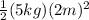
I = 10 kg*m^2

so, we can write the initial equation as:

Mgh =
`(1)/(2)IV^2/R^2 +(1)/(2)MV^2`

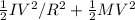
Replacing the data:

(5kg)(9.8)(0.3m) =
`(1)/(2)(10)V^2/(2)^2 +(1)/(2)(5kg)V^2`

solving for V:

(5kg)(9.8)(0.3m) =
`V^2((1)/(2)(10)1/4 +(1)/(2)(5kg))`

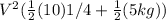
V = 2 m/s