Question

A sample of an unknown gas takes 222 s to diffuse through a porous plug at a given temperature. At the same temperature, N2(g) takes 175 s to diffuse through the same plug. What is the molar mass of the unknown gas?

Answer 1

`\large \boxed{\text{45.1 g/mol}}`

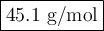
Step-by-step explanation:

Graham’s Law applies to the diffusion of gases:

The rate of diffusion (r) of a gas is inversely proportional to the square root of its molar mass (M).

`r \propto (1)/(√(M))`

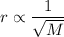
If you have two gases, the ratio of their rates of diffusion is

`(r_(2))/(r_(1)) = \sqrt{(M_(1))/(M_(2))}`

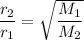
The time for diffusion is inversely proportional to the rate.

`(t_(2))/(t_(1)) = \sqrt{(M_(2))/(M_(1))}`

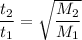
Data:

t₂ = 222 s

t₁ = 175 s

M₁ = 28.01

Calculation :

`\begin{array}{rcl}(222)/(175) & = & \sqrt{(M_(2))/(28.01)}\\\\1.269 & = & \sqrt{(M_(2))/(28.01)}\\\\1.609 & = & (M_(2))/(28.01)\\\\M_(2) & = & 1.609 * 28.01\\ & = & \textbf{45.1 g/mol}\\\end{array}\\\text{The molar mass of the unknown gas is $\large \boxed{\textbf{45.1 g/mol}}$}`