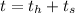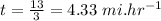Answer:
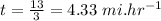
Step-by-step explanation:
Given:
- Distance from the shore,

- distance of house from the shore,
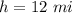
- speed of rowing,
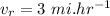
- speed of walking,
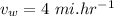
For the least amount of time to reach the house one must row at the nearest point on the shore and then walk from there.
Now the time taken to reach the shore:


Time taken in walking to house from the shore:

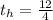
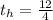
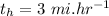
Therefore total time taken: