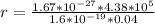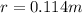Question

A proton starting from rest travels through a potential of 1.0 kV and then moves into a uniform 0.040-T magnetic field directed perpendicular to the path of the proton. What is the radius of the proton’s resulting orbit?

Answer 1

0.114m

Step-by-step explanation:

From the general expression for the radius of the proton's resulting orbit, we have

`r=(mv)/(qB)`

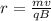
where q is is the charge of the proton
`1.6*10^(-19)C`

m is the mass of the proton
`1.67*10^(-27)kg`

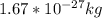
B is the magnetic field
`0.040T`

and v i the speed.

to determine the speed, we use the expression

Kinetic Energy=
`qV`

`1/2mv^(2)=qV`

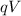
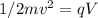
where V is the voltage value i.e 1.0kv

and v is the speed

Hence, from simple rearrangement we have the speed v to be

`v=\sqrt{(2Vq)/(m)} \\`

if we substitute value, we have

`v=\sqrt{(2*1000*1.6*10^(-19) )/(1.67*10^(-27))} \\`

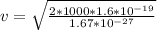
carrying out careful arithmetic we arrive at

`v=4.38*10^(5) m/s`.

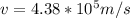using the value for the speed in the expression for the radius of the orbit as stated earlier, we have

`r=(1.67*10^(-27)*4.38*10^(5))/(1.6*10^(-19)*0.04) \\`

`r=0.114m`