Question

What is the value of y? Enter your answer in the box. y = An isosceles triangle with vertices labeled A, B, and C. Side B C is the base. Sides A B and A C are equal. Sides A B and A C are labeled with single tick marks. Angle A is labeled as left parenthesis 4 y plus 10 right parenthesis degrees, angle B is labeled as 75 degrees, and angle C is labeled as left parenthesis 3 x right parenthesis degrees.

Answer 1

5

Explanation:

i took the test

Answer 2

`y = 5`

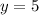
Explanation:

Given:

An isosceles triangle ABC with AB = AC.

∠A =
`(4y+10)\°`

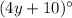
∠B =
`75\°`

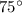
∠C =
`(3x)\°`

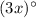
We know that, for an isosceles triangle, the angles opposite equal sides are also equal to each other.

Therefore, ∠B = ∠C

⇒
`75 = 3x`

⇒
`x=(75)/(3)=25`

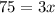
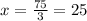
∴ ∠C =
`3* 25=75`°

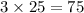Now, the sum of all the interior angles of a triangle is always 180°.

`\angle A + \angle B + \angle C=180\\(4y+10)+75+75=180\\4y+10+150=180\\4y+160=180\\4y=180-160\\4y=20\\y=(20)/(4)=5`

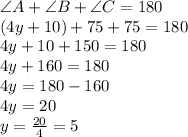
Therefore, the value of 'y' is 5.